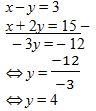|
| http://blogmipa-matematika.blogspot.co.id |
Dalam menentukan penyelesaian SPLDV dapat digunakan metode berikut:
1. Eliminasi.
2. Substitusi.
Kita bahas untuk kedua metode penyelesaian tersebut.
Metode Eliminasi
Eliminasi artinya menghilangkan salah satu variabel dari sistem persamaan linear dengan cara menjumlahkan atau mengurangkan dua buah persamaan linear dalam suatu sistem persamaan.
Dalam menentukan variabel mana yang harus dieliminasi lihat variabel yang koefisiensinya sama, dan jika tidak ada yang sama maka Anda kalikan dengan koefisien-koefisien variabel yang akan dieliminasi secara silang.
Contoh:
Tentukan himpunan penyelesaian SPLDV berikut ini:

Jawab:
Dari soal diketahui bahwa terdapat variabel x yang memiliki koefisien sama maka Anda harus mengeliminasi variabel x untuk memperoleh nilai y, sehingga diperoleh:
Kemudian berdasarkan soal di atas, untuk mengeliminasi variabel y dengan mengalikan secara silang koefisien-koefisien variabel y, diperoleh:
Jadi himpunan penyelesaian SPLDV adalah {(7, 4)}.
Metode Substitusi
Penyelesaian dengan metode substitusi dilakukan dengan cara mengganti salah satu variabel dengan variabel yang lainnya sehingga diperoleh persamaan linear satu variabel.
Contoh:
Tentukan himpunan penyelesaian SPLDV berikut ini:
Jawab:
Berdasarkan persamaan x + 3y = 11 diperoleh x = 11 – 3y. Substitusikan x = 11 – 3y ke persamaan
2x – 5y = – 11 diperoleh
Dengan melakukan substitusi x = 3 ke salah satu persamaan, misal ke persamaan x + 3y = 11
diperoleh
Jadi himpunan penyelesaian SPLDV adalah {(2, 3)}.
Untuk penjelasan lebih terperinci silakan pelajari sumber berikut:
sumber: BSE Matematika SMK kelas 10 karangan H.S. Gumilar tahun 2008.